Generalized, Basis-Independent Kinematic Surface Fitting
Abstract
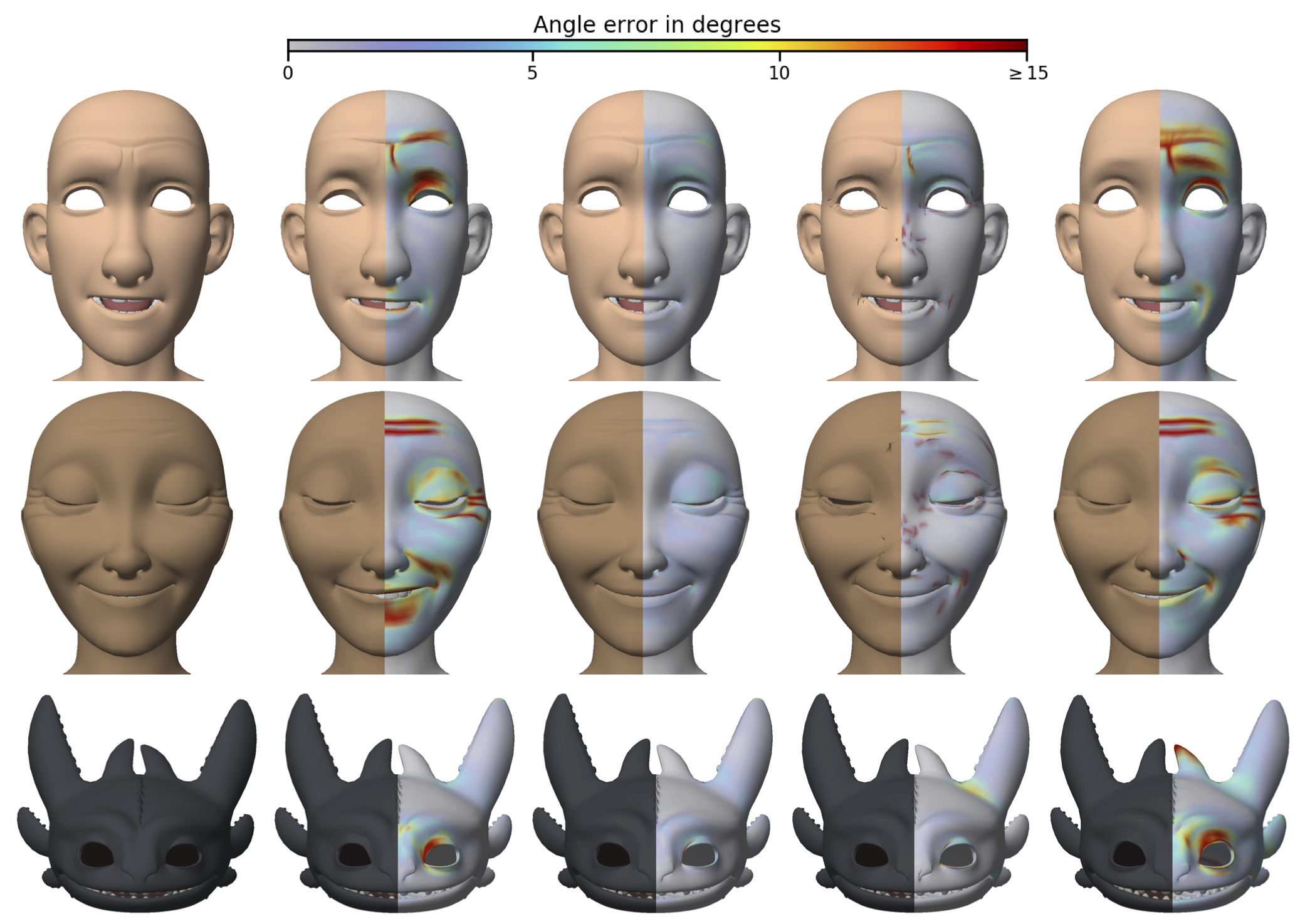
Kinematic surfaces form a general class of surfaces, including surfaces of revolution, helices, spirals, and more. Standard methods for fitting such surfaces are either specialized to a small subset of these surface types (either focusing exclusively on cylinders or exclusively on surfaces of revolution) or otherwise are basis-dependent (leading to scale-dependent results). Previous work has suggested re-scaling data to a fixed size bounding box to avoid the basis-dependence issues. We show that this method fails on some simple, common cases such as a box or a cone with small noise. We propose instead adapting a well-studied approximate maximum-likelihood method to the kinematic surface fitting problem, which solves the basis-dependence issue. Because this technique is not designed for a specific type of kinematic surface, it also opens the door to the possibility of new variants of kinematic surfaces, such as affinely-scaled surfaces of revolution.
Citation
James Andrews and Carlo H. Séquin. "Generalized, Basis-Independent Kinematic Surface Fitting". Computer-Aided Design, 45(3):615–620, March 2013.
Supplemental Material