Analytic Tangent Irradiance Environment Maps for Anisotropic Surfaces
Abstract
We extend spherical harmonic irradiance maps to anisotropic surfaces, replacing Lambertian reflectance with the diffuse term of the popular Kajiya-Kay model. We show that there is a direct analogy, with the surface normal replaced by the tangent. Our main contribution is an analytic formula for the diffuse Kajiya-Kay BRDF in terms of spherical harmonics; this derivation is more complicated than for the standard diffuse lobe. We show that the terms decay even more rapidly than for Lambertian reflectance, going as l-3, where l is the spherical harmonic order, and with only 6 terms (l = 0 and l = 2) capturing 99.8% of the energy. Existing code for irradiance environment maps can be trivially adapted for real-time rendering with tangent irradiance maps. We also demonstrate an application to offline rendering of the diffuse component of fibers, using our formula as a control variate for Monte Carlo sampling.
Citation
Soham Mehta, Ravi Ramamoorthi, Mark Meyer, and Christophe Hery. "Analytic Tangent Irradiance Environment Maps for Anisotropic Surfaces". Computer Graphics Forum, 31(4):1501–1508, June 2012.
Supplemental Material

Figure 1
This is a comparison of our method (anisotropic tangent shading, left) to [Ramamoorthi and Hanrahan 2001] (right), from an interactive session using the Stanford Real-Time Programmable Shading system, in which our rendering algorithm was easily implemented.

Figure 2
Tangents for real objects can be acquired from analysis of images of objects, as described in [Holroyd et al 2008]. We used these tangent maps (left) for our example (right). The Uffizi Gallery environment map is used.

Figure 3
[ Crane et al 2010] descibe how to contruct tangent fields on general geometry. The cat example from this work (tangent field to the left) was shaded using our algorithm (right). The Grace Cathedral environment map is used.
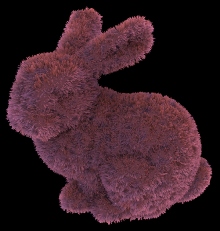
Figure 4
The furry bunny model has 1.2M triangles. Our algorithm runs in real time for complex geometry. The Grace Cathedral environment map is used.
Acknowledgements:
Milos Hasan Paul Debevec's Light Probe Gallery