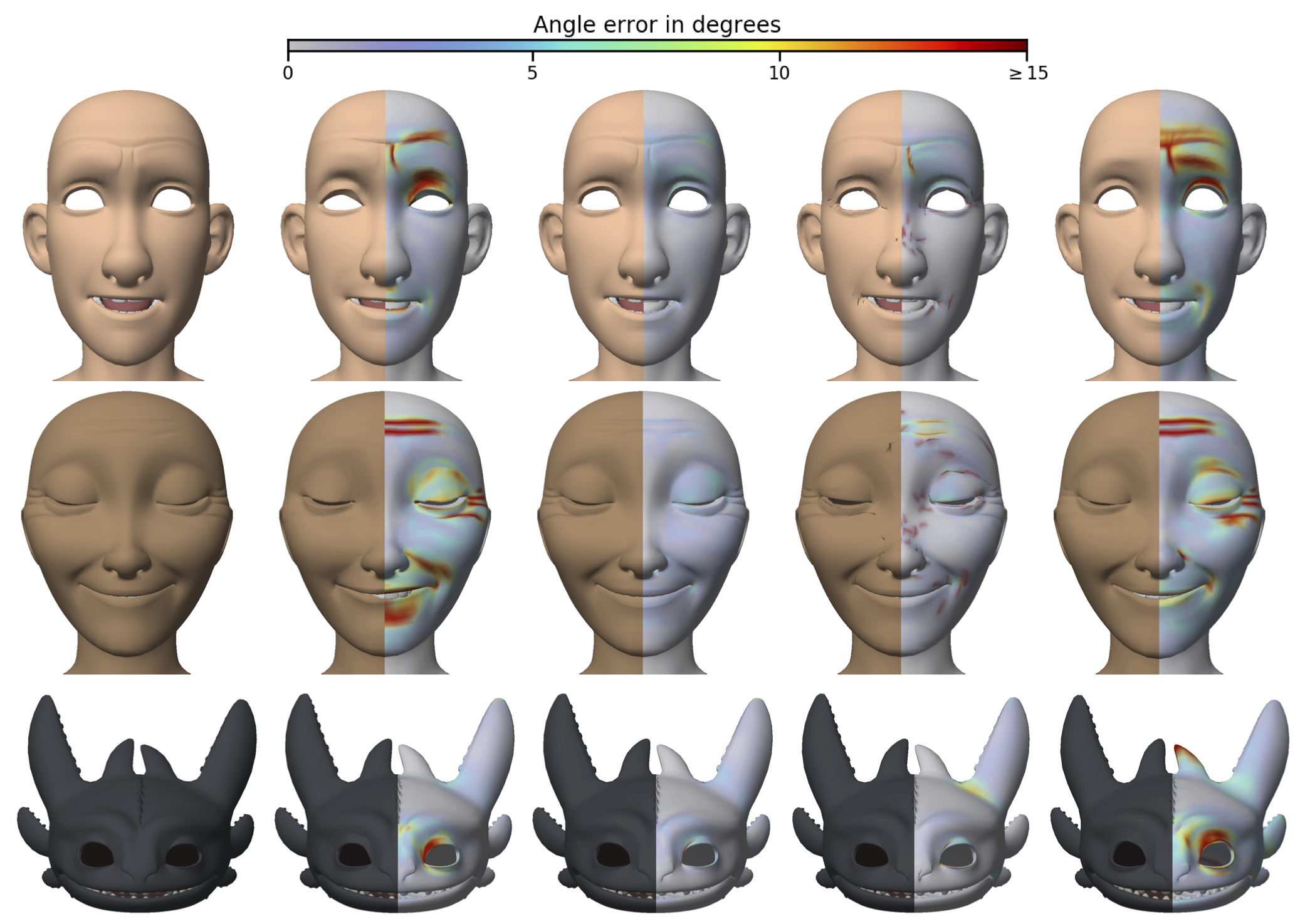
Interpolating and Approximating Implicit Surfaces from Polygon Soup
Abstract
This paper describes a method for building interpolating or approximating implicit surfaces from polygonal data. The user can choose to generate a surface that exactly interpolates the polygons, or a surface that approximates the input by smoothing away features smaller than some user-specified size. The implicit functions are represented using a moving least-squares formulation with constraints integrated over the polygons. The paper also presents an improved method for enforcing normal constraints and an iterative procedure for ensuring that the implicit surface tightly encloses the input vertices.
Citation
Chen Shen, James F. O'Brien, and Jonathan R. Shewchuk. "Interpolating and Approximating Implicit Surfaces from Polygon Soup". In Proceedings of ACM SIGGRAPH 2004, pages 896–904. ACM Press, August 2004.
Supplemental Material

Full Paper Movie
Full length video to acompany paper. Encoded with DIVX.
Example Images
Examples |
|||||||||||
|
|
|
Least Square |
Moving
Least Square |
 |
 |
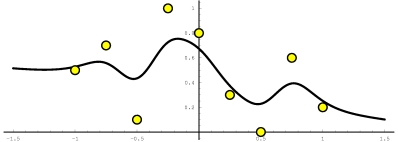 |
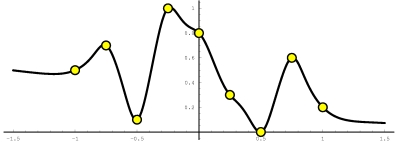
Moving least square method is an
extension of standard least square fit method. It can provide either
interpolating or approximating behaviors.
| Pseudo-normal
Constraints |
True-normal
Constraints |
 |
 |
 |
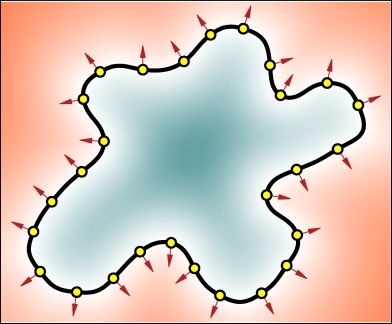 |
Comparison between the widely used
pseudo-normal constraints method and our new true-normal constraints
method. Left images show the results generated by pseudo-normal
constraints. The "+" and "-" signs indicate the placement of the inside
and outside pseudo-normal constraints. Right images show the results
with out new true-normal constraints method and the arrows indicate the
outward normal directions.
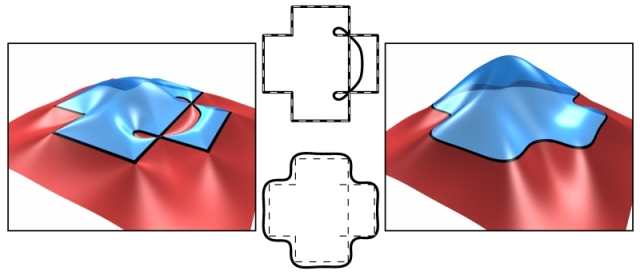
A two-dimensional example comparing interpolating and
approximating results. The center images show input constraints as
dotted lines and the contour as a solid line. The outer images show the
resulting function as a height-field.
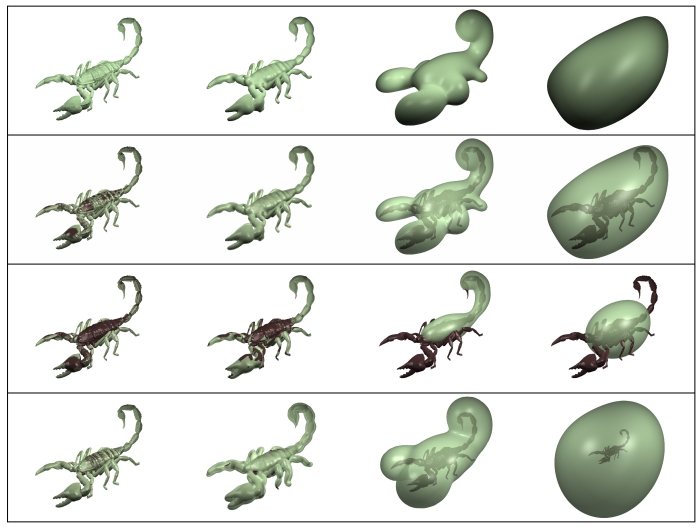
The first (top) row shows the
result of applying our iterative adjustment algorithm with different
values of Epsilon to a polygonal scorpion model. The second row
shows the original and constructed surfaces together. The third row
shows the result of only adjusting the surface to average values (no
iterative adjustment). The fourth row shows the result generated
when no correction is applied.

The top left image shows a polygonized version the Utah teapot which contains holes (around lid and tip of spout), and intersecting parts (handle and spout with body). The top right image is a near-interpolating surface which fills the holes and removes intersecting surfaces. The bottom row contains photographs of physical models built on a fused deposition machine. The bottom right image shows a physical cutaway model.

The far-left image shows a
closeup view of the original polygons for the heavy-loader's back
grill. The center-left image shows the resulting interpolating
surface, and the center-right a slightly approximating one. The
far-right image shows a rear view of the interpolating surface for the
entire loader. The dented appearance near sharp edges is a
polygonization artifact.

The heavy-loader shown top left
contains many defects that make it unsuitable for simulation as a
deformable object. The approximating surface, top center, fully
encloses the original model. The tetrahedral finite-element
model, top right, can be used as a simulation envelope to model the
effect of an impact, lower left and lower right.