Refolding Planar Polygons
Abstract
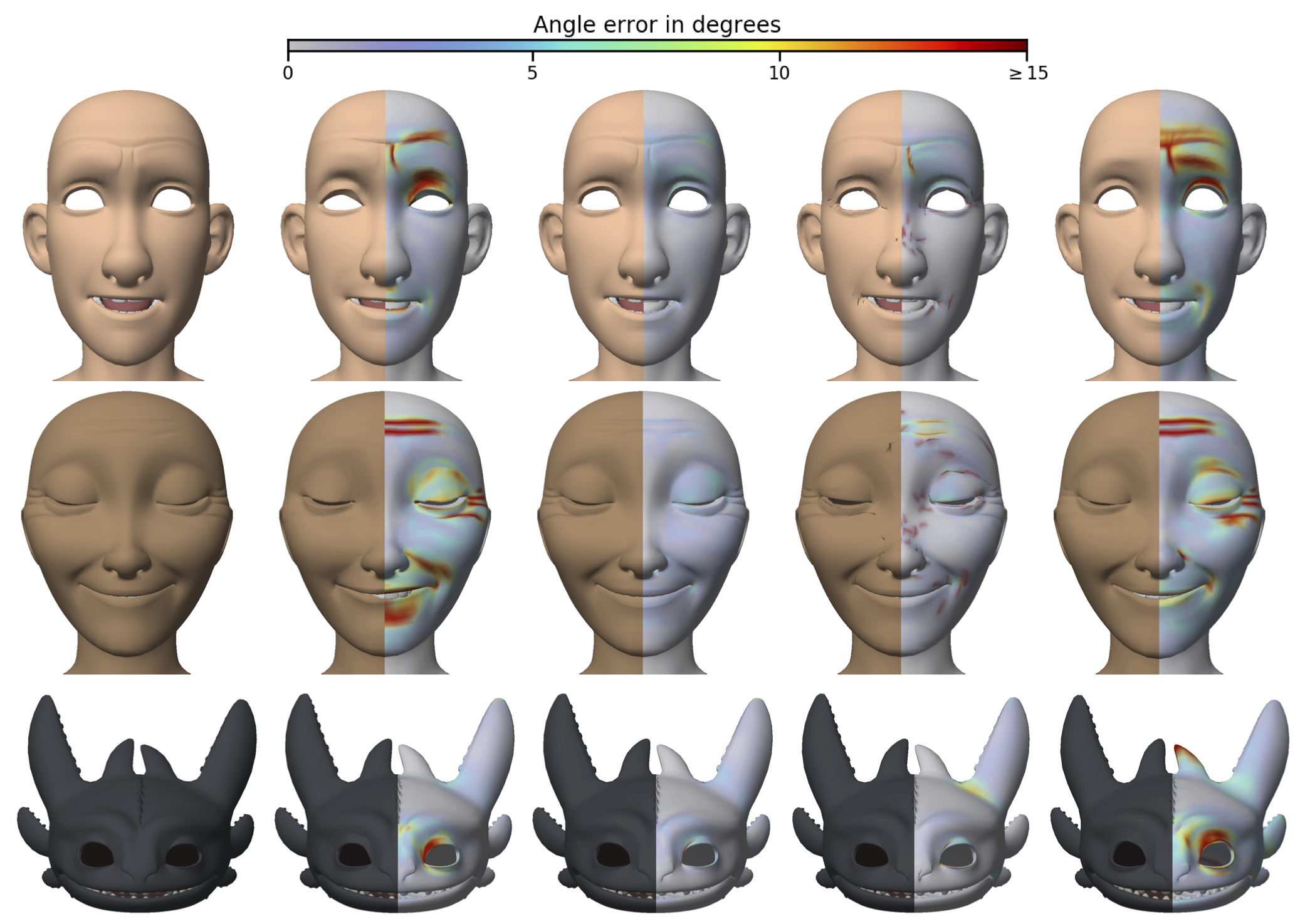
This paper describes an algorithm for generating a
guaranteed-intersection-free interpolation sequence between any pair
of compatible polygons. Our algorithm builds on prior results from
linkage unfolding, and if desired it can ensure that every edge
length changes monotonically over the course of the interpolation
sequence. The computational machinery that ensures against
self-intersection is independent from the distance metric that
determines the overall character of the interpolation sequence.
This approach provides a powerful control mechanism for determining
how the interpolation should appear, while still assuring against
intersection and guaranteeing termination of the algorithm. Our
algorithm also allows additional control by accommodating set of
algebraic constraints that can be weakly enforced throughout the
interpolation sequence.
Awarded best paper at SoCG 2006.
Citation
Hayley N. Iben, James F. O'Brien, and Eric D. Demaine. "Refolding Planar Polygons". In Proceedings of the 22th Annual Symposium on Computational Geometry, pages 71–79, June 2006.
Supplemental Material
Full Movie (55 Mb)
Encoded with Quicktime MPEG-4. (Quicktime version 6 or higher is needed to view it.)

Example Sequence
An intersection-free interpolation sequence generated using our algorithm. For this example, all edge lengths were held constant, the linear interpolation of vertex positions was used for the direction heuristic, and the total computation time was 1.6 minutes on a 3.06 GHz Pentium IV computer with 1 GB of memory.

Edge Lengths Constrained

Edge Lengths Unconstrained
This example interpolates between two configurations of interlocked teeth. The top row shows the result computed with the edge lengths constrained to change monotonically and required 5.0 minutes of computation. The bottom row shows the result computed with unconstrained edge lengths and required 1.8 minutes of computation.