A Theory of Differential Photometric Stereo for Unknown BRDFs
Abstract
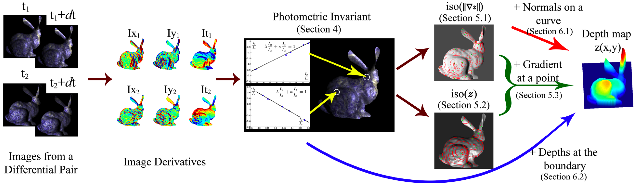
We present a comprehensive theory of photometric surface reconstruction from image derivatives. For unknown isotropic BRDFs, we show that two measurements of spatial and temporal image derivatives, under unknown light sources on a circle, suffice to determine the surface. This result is the culmination of a series of fundamental observations. First, we discover a photometric invariant that relates image derivatives to the surface geometry, regardless of the form of isotropic BRDF. Next, we show that just two pairs of differential images from unknown light directions suffice to recover surface information from the photometric invariant. This is shown to be equivalent to determining isocontours of constant magnitude of the surface gradient, as well as isocontours of constant depth. Further, we prove that specification of the surface normal at a single point completely determines the surface depth from these isocontours. In addition, we propose practical algorithms that require additional initial or boundary information, but recover depth from lower order derivatives. Our theoretical results are illustrated with several examples on synthetic and real data.
Citation
Manmohan Chandraker, Jiamin Bai, and Ravi Ramamoorthi. "A Theory of Differential Photometric Stereo for Unknown BRDFs". In IEEE Conference on Computer Vision and Pattern Recognition, pages 2505–2512, 2011.
Supplemental Material
Tech Report
This tech report contains detailed proofs, as well as descriptions of our experiments, acquisition setup and numerical implementation.