An Energy-Driven Approach to Linkage Unfolding
Abstract
We present a new algorithm for unfolding planar polygonal linkages without self-intersection based on following the gradient flow of a "repulsive" energy function. This algorithm has several advantages over previous methods. (1) The output motion is represented explicitly and exactly as a piecewise-linear curve in angle space. As a consequence, an exact snapshot of the linkage at any time can be extracted from the output in strongly polynomial time (on a real RAM supporting arithmetic, sin and arcsin). (2) Each linear step of the motion can be computed exactly in O(n2) time on a real RAM where n is the number of vertices. (3) We explicitly bound the number of linear steps (and hence running time) as a polynomial in n and the ratio between the maximum edge length and the initial minimum distance between a vertex and an edge. (4) Our method is practical and easy to implement. We provide a publicly accessible Java applet that implements the algorithm.
Best paper award at SoCG 2004.
Citation
Jason H. Cantarella, Eric D. Demaine, Hayley N. Iben, and James F. O'Brien. "An Energy-Driven Approach to Linkage Unfolding". In Proceedings of the 20th Annual Symposium on Computational Geometry, June 2004.
Supplemental Material

Teeth with energy method.

Tree with energy method.

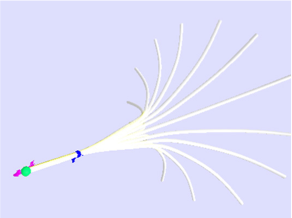
A spiral open chain.

Tentacle opening.

Spider shape opening.
Demonstration Applet
If your browser does not support the JRE plugin, then you may still be able to run this applet by installing the Java J2SE v 1.4 SDK and running the command "appletviewer" with this URL as the first argument in quotes: appletviewer "http://url_of_this_page.html" where you replace url_of_this_page with this page's address.