A Dual Theory of Inverse and Forward Light Transport
Abstract
We present the theoretical and computational foundations for inverse light transport as a dual of forward rendering. Inverse light transport seeks to undo global illumination effects, such as interreflections, that pervade images of most scenes. Mathematically, this duality is established through the existence of underlying Neumann series expansions. Physically, we show that each term of our inverse series cancels an interreflection bounce, just as the forward series adds them. While the convergence properties of the forward series are well-known, we show that the oscillatory convergence of the inverse series leads to more interesting conditions on material reflectance. Conceptually, the inverse problem requires the inversion of a large transport matrix, which is impractical for realistic resolutions. A natural consequence of our theoretical framework is a suite of fast computational algorithms for light transport inversion - analogous to finite element radiosity, Monte Carlo and wavelet-based methods in forward rendering - that rely at most on matrix-vector multiplications. We demonstrate two practical applications, namely, separation of individual bounces of the light transport and fast projector radiometric compensation to display images free of global illumination artifacts in real-world environments.
Citation
Jiamin Bai, Manmohan Chandraker, Tian-Tsong Ng, and Ravi Ramamoorthi. "A Dual Theory of Inverse and Forward Light Transport". In European Conference on Computer Vision, pages 1–8, 2010.
Supplemental Material
Tech Report
This tech report contains detailed derivations, experiments and discussions on the generality and limitations of our theory.

Application: Fast Radiometric Compensation
The fast algorithms presented in this paper can be used to achieve desired projector outputs, free of global illumination artifacts, even in scenes with complex geometry and reflectances. Our prototype Matlab implementation for the iterative finite element method can invert 130K x 130K light transports in 3 seconds.

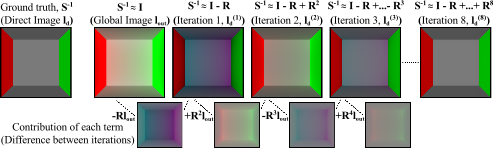
Application: Fast Direct-Global Recovery and Bounce Separation
Another application is to efficiently separate observed images into direct and global components, as well as recover each bounce of global illumination.

Video
A video demonstrating the bounce separation application.